Shortcut: WD:MATHWikidata:WikiProject Mathematics
Goals
[edit]Long term goals
[edit]- Organize data about mathematics
Short term goals
[edit]- Review the #Scope
- Use maintained by WikiProject (P6104) on all items and properties within #Scope
- Use field of usage (P9488) on senses of lexemes within #Scope (uses)
- Use the property has facet polytope (P1312) on all applicable items (7/??), and create missing items
- Gather information from infoboxes
- Create more properties that semantically describe items
- Create featured items that show how properties should be used
- Create "has part" property entries for formula components / identifiers -> discussion
Scope
[edit]- All Wikidata properties for which instance of (P31) has the value Wikidata property related to mathematics (Q22988631)

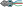
 (see list).
(see list). - All Wikidata entities with a statement that involves any of these properties.
- Auxiliary wiki pages that assist with the above.
Infoboxes
[edit]- Category:Mathematics infobox templates (Q8612039)
- Infobox Méthode scientifique (Infobox scientific method) for French Wikipedia (Q8447)
- Infobox Discipline for French Wikipedia (Q8447)
Useful lists and queries
[edit]- List of integers in Wikidata
- Subclass tree for number (Q11563): http://tools.wmflabs.org/wikidata-todo/tree.html?q=11563&rp=279&lang=en
- Table of all theorems
- pairs of equivalent theorems / axioms / principles (using loops of generalization of (P7719)
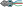 )
)
- pairs of equivalent theorems / axioms / principles (using loops of generalization of (P7719)
- Table of notable numbers
- Uses of OEIS ID
Error detection: please make sure the query below returns zero results, and fix any item that appears.
- Numbers that are defined as a sub-class of something.
- list of prime numbers
- list of Mersenne numbers and Mersenne primes
- list of dates of factorization
Properties
[edit]See also: List of properties related to mathematics (SPARQL query), Template:Mathematics properties (manually curated), List of mathematics-related Wikidata properties by usage count (SPARQL query) and Wikidata:List of properties/mathematics (bot-generated list)
Properties used in Wikipedia
[edit]The following properties are available in Wikipedia, Wikiversity, and other Wikimedia wikis and are displayed when clicking on the annotated formulae. See w:Help:Displaying_a_formula#Semantics_and_links for a more detailed documentation. The assumption when implementing the semantics feature in mw:Extension Math was that relations or formulae like the Mass-Energy-Equivalence are annotated on Wikidata.
| Title | ID | Data type | Description | Examples | Inverse |
|---|---|---|---|---|---|
| defining formula | P2534 | Mathematical expression | formula: mathematical formula representing a theorem or law. Maximum length: 400 characters | ideal gas law <defining formula> | - |
| has part(s) | P527 | Item | has part, consist of and meronymy: part of this subject; inverse property of "part of" (P361). See also "has parts of the class" (P2670). | ideal gas law <has part(s)> pressure | part of |
| quantity symbol (string) | P416 | String | quantity symbol: symbol for a mathematical or physical quantity | electric charge <quantity symbol (string)> Q and q | - |
General Properties
[edit]As opposed to the properties above that are used for semantic annotations in Wikipedia the following properties are used under the assumption that the corresponding wikidata item defines a mathematical/physical concept which has a definiendum that can be derived (calculated from) other symbols.
| Title | ID | Data type | Description | Examples | Inverse |
|---|---|---|---|---|---|
| defining formula | P2534 | Mathematical expression | formula: mathematical formula representing a theorem or law. Maximum length: 400 characters | Pythagorean theorem <defining formula> | - |
| in defining formula | P7235 | Mathematical expression | variable: any symbol used in the defining formula (P2534) | f-number <in defining formula> | - |
| quantity symbol (LaTeX) | P7973 | Mathematical expression | quantity symbol: symbol for a mathematical or physical quantity in LaTeX | electric charge <quantity symbol (LaTeX)> | - |
| calculated from | P4934 | Item | calculation: value of the subject item cannot be measured directly or can be calculated from the following measurands or attributes | body mass index <calculated from> human body weight and human height | - |
| relative to | P2210 | Item | reference point: qualifier: what a statement value is relative to | FTCS scheme <has part(s)> Euler method <relative to> time | - |
| studied in | P2579 | Item | academic discipline: subject is studied by this science or domain | numerical method <studied in> numerical analysis | is the study of |
| has characteristic | P1552 | Item | quality: inherent or distinguishing quality or feature of the entity. Use a more specific property when possible | mathematical proof <has characteristic> validity | - |
| notation | P913 | Item | notation: mathematical notation or another symbol | equality <notation> equals sign | - |
| statement describes | P2384 | Item | formalization of the statement contains a bound variable in this class | Pythagorean theorem <statement describes> right triangle | - |
| admissible rule in | P2577 | Item | admissible rule: this logic inference rule is admissible in that logical system | modus ponens <admissible rule in> classical logic | - |
| generalization of | P7719 | Item | logical implication and extension: statement logically implied by the subject or a similar algorithm/function whose domain is a subset of the subject's domain | law of cosines <generalization of> Pythagorean theorem | - |
| is invariant under | P12457 | Item | invariant: subject is unchanged by this process / function / group of transformation | graph property <is invariant under> graph isomorphism | - |
Numbers
[edit]| Title | ID | Data type | Description | Examples | Inverse |
|---|---|---|---|---|---|
| numeric value | P1181 | Quantity | numeric value and quantity value: numerical value of a number, a mathematical constant, or a physical constant | golden ratio <numeric value> 1,6180339887±0,0000000001 | - |
| prime factor | P5236 | Item | prime factor: one of the prime numbers that can be multiplied to give this number | 2334 <prime factor> 2, 389 and 3 | - |
| greater than | P5135 | Item | greater than: instances of the item have a greater value than corresponding instances of the object, for the given measure | em dash <greater than> en dash | less than |
| less than | P5136 | Item | less than: instances of the item have a lesser value than corresponding instances of the object, for the given measure | aerostat <less than> air | greater than |
| number of decimal digits | P7316 | Quantity | numerical digit: number of decimal digits of a natural number | 10^90 <number of decimal digits> 91 | - |
| radix | P3264 | Item | radix: number of distinct digits in a positional numeral system | hexadecimal <radix> 16 | - |
Mathematicans and Mathematical History
[edit]| Title | ID | Data type | Description | Examples | Inverse |
|---|---|---|---|---|---|
| discoverer or inventor | P61 | Item | inventor, innovator, discoverer, discovery, invention and discoveries and inventions: subject who discovered, first described, invented, or developed this discovery or invention or scientific hypothesis or theory | Poincaré conjecture <discoverer or inventor> Henri Poincaré | - |
| time of discovery or invention | P575 | Point in time | invention, discovery and archaeological find: date or point in time when the item was discovered or invented | Euler method <time of discovery or invention> 1768 | - |
| named after | P138 | Item | eponym, memorial society and namesakes: entity or event that inspired the subject's name, or namesake (in at least one language). Qualifier "applies to name" (P5168) can be used to indicate which one | Euler method <named after> Leonhard Euler | - |
| proved by | P1318 | Item | person who proved something | Poincaré conjecture <proved by> Grigori Perelman | - |
| solved by | P1136 | Item | person that solved a scientific question | Fermat's Last Theorem <solved by> Andrew Wiles | - |
| based on | P144 | Item | based on: the work(s) or inputs used as the basis for subject item | first Pythagorean trigonometric identity <based on> Pythagorean theorem | derivative work |
| Erdős number | P2021 | Quantity | Erdős number: the "collaborative distance" between mathematician Paul Erdős and another person. Use point in time (P585) as qualifier and should be used with a source. | Paul Erdős <Erdős number> 0 | - |
| title in LaTeX | P6835 | Mathematical expression | LaTeX: (qualifier) for title property (P1476), to write title in LaTeX/math notation, if the string can't render it normally. Enclose normal text with "\text{" and "}" | On the Integers of the Form xk +yk <title in LaTeX> | - |
Sets, Algebras, and Topology
[edit]| Title | ID | Data type | Description | Examples | Inverse |
|---|---|---|---|---|---|
| cardinality of this set | P2820 | Item | cardinality: measure of number of elements of a set | rational number <cardinality of this set> aleph null | - |
| group cardinality | P1164 | Quantity | group order: number of elements in a finite group in mathematics | dihedral group of order 6 <group cardinality> 6 | - |
| identity element | P8864 | Item | identity element: value of the identity element of the mathematical operation | addition <identity element> zero | - |
| has operator | P8866 | Item | operator: mathematical operator associated with this algebraic structure | additive group <has operator> addition | - |
| mathematical inverse | P8865 | Item | inverse: inverse element with respect to binary operation given as a qualifier using P2210 | 2 <mathematical inverse> ½ | mathematical inverse |
| contains | P4330 | Item | insertion: item or substance located within this item but not part of it | sphere <contains> open ball | location |
| has part(s) of the class | P2670 | Item | has parts of class: the subject has one or more parts of the object class | set of real numbers <has part(s) of the class> real number | - |
| graph radius | P7391 | Quantity | graph radius: the minimum eccentricity of any vertex of a graph | claw graph <graph radius> 1 | - |
| underlying structure(s) | P12322 | Item | underlying structure: mathematical structure(s) obtained by deleting some data of the subject | metric space <underlying structure(s)> metrizable space | - |
To model whether a set is open or closed, use
For a class item that is a union of other items, use
- real number (Q12916)union of (P2737)list of values as qualifiers (Q23766486)
of (P642)irrational number (Q607728), rational number (Q1244890), integer (Q12503), - real number (Q12916)disjoint union of (P2738)list of values as qualifiers (Q23766486)
of (P642)irrational number (Q607728), rational number (Q1244890).
Knots and Links
[edit]| Title | ID | Data type | Description | Examples | Inverse |
|---|---|---|---|---|---|
| crossing number | P11035 | Quantity | crossing number: crossing number for mathematical knots; the crossing number of a knot is the smallest number of crossings of any diagram of the knot. It is a knot invariant. | unknot <crossing number> 0 | - |
| Alexander polynomial | P5350 | Mathematical expression | Alexander polynomial: invariant of a knot or link. Use 't' as variable and list monomials in decreasing order. | unknot <Alexander polynomial> | - |
| Conway polynomial | P5351 | Mathematical expression | Conway–Alexander polynomial: invariant of a knot. Use z as variable and list monomials in decreasing order. | unknot <Conway polynomial> | - |
| Jones polynomial | P5352 | Mathematical expression | Jones polynomial: invariant of a knot or link. Use q as variable and list monomials in decreasing order. | unknot <Jones polynomial> | - |
| Alexander–Briggs notation | P6432 | Mathematical expression | Alexander-Briggs notation: common notation of abstract knots and links | unknot <Alexander–Briggs notation> | - |
| Dowker-Thistlethwaite notation | P8378 | Mathematical expression | Dowker–Thistlethwaite notation: descriptive property of mathematical knots, also known as Dowker notation | trefoil knot <Dowker-Thistlethwaite notation> | - |
| Dowker-Thistlethwaite name | P8416 | Mathematical expression | Dowker–Thistlethwaite name: unambiguous systematic identifier scheme for mathematical knots | unknot <Dowker-Thistlethwaite name> | - |
| Gauss notation | P11034 | Mathematical expression | Gauss notation: Gauss notation for knots and links | unknot <Gauss notation> not applicable | - |
Methods and Algorithms
[edit]| Title | ID | Data type | Description | Examples | Inverse |
|---|---|---|---|---|---|
| computes solution to | P2159 | Item | problem that this algorithm or method solves | DPLL algorithm <computes solution to> boolean satisfiability problem | - |
| solution to | P9030 | Item | a mathematical object that satisfies the criteria for a mathematical problem | eigenvalue <solution to> characteristic equation | - |
| uses | P2283 | Item | use: item or concept used by the subject or in the operation (see also instrument [P1303] and armament [P520]) | method of lines <uses> discretization | used by |
| approximation algorithm | P1171 | Item | approximation algorithm: method used to approximate a number | pi <approximation algorithm> Gauss–Legendre algorithm | - |
| computational complexity | P10374 | Item | computational complexity: the most specific complexity class this computational problem has been proved to belong to; if available, provide the tight complexity, otherwise both hardness and membership can be specified | st-connectivity <computational complexity> NL-complete | - |
| best-case time complexity | P3753 | Mathematical expression | time complexity: time complexity of an algorithm at least | quicksort <best-case time complexity> | - |
| average time complexity | P3754 | Mathematical expression | time complexity: time complexity of an algorithm on average | quicksort <average time complexity> | - |
| worst-case time complexity | P3752 | Mathematical expression | time complexity: time complexity of an algorithm at most | quicksort <worst-case time complexity> | - |
| best-case space complexity | P3756 | Mathematical expression | space complexity: space complexity of an algorithm at least | merge sort <best-case space complexity> | - |
| average space complexity | P3757 | Mathematical expression | space complexity: space complexity of an algorithm on average | quicksort <average space complexity> | - |
| worst-case space complexity | P3755 | Mathematical expression | space complexity: space complexity of an algorithm at most | quicksort <worst-case space complexity> | - |
| Butcher tableau | P8558 | Mathematical expression | Butcher tableau: table containing the coefficients of a Runge-Kutta method | backward Euler method <Butcher tableau> | - |
The following are also useful for iterative numerical methods
- Euler method (Q868454)has characteristic (P1552)order of convergence (Q97940482)
numeric value (P1181)"1" - Euler method (Q868454)has characteristic (P1552)number of steps (Q98293869)
quantity (P1114)"1" (number of steps (Q98293869): number of previous steps used in an iterative numerical method to calculate the next iteration) - Euler method (Q868454)has characteristic (P1552)number of stages (Q97672364)
quantity (P1114)"1" (number of stages (Q97672364): the number of stages in a Runge-Kutta method) - backward Euler method (Q2736820)has characteristic (P1552)L-stability (Q277932)
- Euler method (Q868454)does not have characteristic (P6477)A-stability (Q65926322)
Functions
[edit]| Title | ID | Data type | Description | Examples | Inverse |
|---|---|---|---|---|---|
| definition domain | P1568 | Item | domain of a function: set of "input" or argument values for which a mathematical function is defined | square function <definition domain> real number | - |
| codomain | P1571 | Item | codomain: codomain of a function | square function <codomain> real number | - |
| image of function | P2396 | Item | image: set of values that a mathematical function actually takes | square function <image of function> set of non-negative real numbers | - |
| input set | P1851 | Item | input set: a superset of the domain of a function or relation that may include some inputs for which the function is not defined; to specify the set of only those inputs for which the function is defined use domain (P1568) | tangent <input set> set of real numbers | - |
| support of a function | P10731 | Mathematical expression | support: subset of the domain containing those elements which are not mapped to zero | normal distribution <support of a function> | - |
| power series expansion | P10969 | Mathematical expression | power series expansion: power series expansion of the subject | exponential function <power series expansion> | - |
Several properties of functions are modeled in Wikdata using the has characteristic (P1552) and does not have characteristic (P6477) properties.
- cosine (Q1256164)has characteristic (P1552)boundedness (Q60644809)
- exponential function (Q168698)has characteristic (P1552)monotonicity (Q78056921)
- cosine (Q1256164)does not have characteristic (P6477)monotonicity (Q78056921)
- square function (Q3075175)has characteristic (P1552)arity (Q1315869)
numeric value (P1181)"1"
To specify symmetry, use
- cosine (Q1256164)instance of (P31)even function (Q12138960)
- sine (Q152415)instance of (P31)odd function (Q18088516)
Geometry
[edit]| Title | ID | Data type | Description | Examples | Inverse |
|---|---|---|---|---|---|
| has facet polytope | P1312 | Item | facet: facet of a polytope, in the next-lower dimension | dodecahedron <has facet polytope> pentagon | - |
| has vertex figure | P1678 | Item | vertex figure: the figure exposed when a corner of a polytope is sliced off | cuboctahedron <has vertex figure> rectangle | - |
| base | P3263 | Item | base and base face: configuration of a polytop vertices around the symmetry axis | pentagonal prism <base> pentagon | - |
| Euler characteristic | P6438 | Quantity | Euler characteristic: topological invariant of a space; the alternating sum of the dimensions of the (co)homology of a space | sphere <Euler characteristic> 2 | - |
| dual to | P1322 | Item | duality, dual polytope and dual graph: dual of a polytope, graph or curve | cube <dual to> octahedron | dual to |
| Schläfli symbol | P3228 | String | Schläfli symbol: notation that defines regular polytopes and tessellations | regular polygon <Schläfli symbol> {n} | - |
| Schläfli symbol | P3228 | String | Schläfli symbol: notation that defines regular polytopes and tessellations | regular polygon <Schläfli symbol> {n} | - |
| is invariant under | P12457 | Item | invariant: subject is unchanged by this process / function / group of transformation | regular icosahedron <is invariant under> icosahedral symmetry | - |
Probability
[edit]invalid 'id' parameter should be a number or 'new', none provided
| Title | ID | Data type | Description | Examples | Inverse |
|---|---|---|---|---|---|
| probability mass function | P10732 | Mathematical expression | probability mass function: function that gives the probability that a discrete random variable is exactly equal to some value | Poisson distribution <probability mass function> | - |
| cumulative distribution function | P10736 | Mathematical expression | distribution function: probability that X will take a value less than or equal to x | normal distribution <cumulative distribution function> | - |
| quantile function | P10737 | Mathematical expression | quantile function: value at which the probability of the random variable is less than or equal to the given probability | normal distribution <quantile function> | - |
| mean of a probability distribution | P10738 | Mathematical expression | mean: long-run average value of repetitions of the experiment it represents | normal distribution <mean of a probability distribution> | - |
| median of a probability distribution | P10739 | Mathematical expression | median: value separating the higher half of a data sample, a population, or a probability distribution, from the lower half | normal distribution <median of a probability distribution> | - |
| mode of a probability distribution | P10740 | Mathematical expression | mode: value that appears most often in a set of data | normal distribution <mode of a probability distribution> | - |
| variance of a probability distribution | P10743 | Mathematical expression | variance: expectation of the squared deviation of a random variable from its mean | normal distribution <variance of a probability distribution> | - |
| skewness | P10744 | Mathematical expression | coefficient of skewness: measure of the asymmetry of the probability distribution of a real-valued random variable about its mean | normal distribution <skewness> | - |
| excess kurtosis | P10745 | Mathematical expression | excess kurtosis: measure of the "tailedness" of the probability distribution of a real-valued random variable | normal distribution <excess kurtosis> | - |
| information entropy | P10746 | Mathematical expression | information entropy: expected value (average) of the information contained in each message | normal distribution <information entropy> | - |
| moment-generating function | P10747 | Mathematical expression | moment-generating function: alternative specification of its probability distribution | normal distribution <moment-generating function> | - |
| characteristic function | P10735 | Mathematical expression | characteristic function: Fourier transform of the probability density function | normal distribution <characteristic function> | - |
| Fisher information | P10734 | Mathematical expression | Fisher information: way of measuring the amount of information that an observable random variable X carries about an unknown parameter θ of a distribution that models X | normal distribution <Fisher information> | - |
| probability generating function | P10733 | Mathematical expression | probability-generating function: power series representation (the generating function) of the probability mass function of the random variable | Poisson distribution <probability generating function> | - |
| support of a function | P10731 | Mathematical expression | support: subset of the domain containing those elements which are not mapped to zero | normal distribution <support of a function> | - |
Graph theory
[edit]| Title | ID | Data type | Description | Examples | Inverse |
|---|---|---|---|---|---|
| graph diameter | P7462 | Quantity | graph diameter: maximum eccentricity of any vertex in the graph | claw graph <graph diameter> 2 | - |
| graph girth | P8986 | Quantity | girth: length of a shortest cycle contained in the graph | double-star snark <graph girth> 6 | - |
| graph radius | P7391 | Quantity | graph radius: the minimum eccentricity of any vertex of a graph | claw graph <graph radius> 1 | - |
| The House of Graphs ID | P12934 | External identifier | House of Graphs: ID for an undirected graph on houseofgraphs.org | triangle graph <The House of Graphs ID> 1374 | - |
External Identifiers
[edit]| Title | ID | Data type | Description | Examples | Inverse |
|---|---|---|---|---|---|
| OEIS ID | P829 | External identifier | On-Line Encyclopedia of Integer Sequences: identifier on the On-Line Encyclopedia of Integer Sequences | Fermat number <OEIS ID> A000215 | - |
| Mathematics Genealogy Project ID | P549 | External identifier | identifier for mathematicians and computer scientists at the Mathematics Genealogy Project | Patrick Ion <Mathematics Genealogy Project ID> 8691 | - |
| zbMATH author ID | P1556 | External identifier | identifier of a person in the Zentralblatt MATH database | Patrick Ion <zbMATH author ID> ion.patrick-d-f | - |
| zbMATH Open document ID | P894 | External identifier | identifier in the zbMATH Open database | Game Theory: A Multi-Leveled Approach <zbMATH Open document ID> 1147.91001 | - |
| MathWorld ID | P2812 | External identifier | MathWorld: identifier for entries in MathWorld, online mathematics reference work | aleph null <MathWorld ID> Aleph-0 | - |
| nLab ID | P4215 | External identifier | name of a page in nLab wiki | total order <nLab ID> total order | - |
| ProofWiki ID | P6781 | External identifier | identifier for a ProofWiki article | Euclid's theorem <ProofWiki ID> Euclid's Theorem | - |
| Encyclopedia of Mathematics article ID | P7554 | External identifier | identifier for an article on the Encyclopedia of Mathematics wiki (encyclopediaofmath.org) | Cauchy–Schwarz inequality <Encyclopedia of Mathematics article ID> Cauchy_Schwarz_inequality | - |
| Mathematical Reviews ID | P889 | External identifier | identifier in Mathematical Reviews, a journal and online database | Introduction to the Theory of Games <Mathematical Reviews ID> 50248 | - |
Polytopes
[edit]| Root item | Query | Query description | Count date | Count quantity | Count link |
|---|---|---|---|---|---|
| polytope (Q747980) | tree[747980][][279] | subclasses | 2014-10-07 | 813 | autolist2 |
| vertex (Q26401) | web[26401][1312] | polytopes with property "has facet polytope" (direct, not inherited) | 2014-10-07 | 534 | autolist2 |
Participants
[edit]The participants listed below can be notified using the following template in discussions:{{Ping project|Mathematics}}
- Opensofias
- Tobias1984
- Arthur Rubin
- Cuvwb
- TomT0m
- Physikerwelt
- Lymantria
- Bigbossfarin
- Infovarius
- Helder
- PhilMINT
- Malore
- Lore.mazza51
- Wikisaurus
- The Anome
- The-erinaceous-one
- Daniel Mietchen
- Haansn08
- Xenmorpha
- John Samuel
- Jeremy Dover
- Toni 001
- Bocardodarapti
- Duckmather
- HTinC23
- fgnievinski
- Paul-Olivier Dehaye
- uni
- Dexxor
Userbox
[edit]- See: Wikidata:Userboxes
| This user is a member of WikiProject Mathematics |
Subpages
[edit]This WikiProject has the following subpages:
- 1000+Theorems
- 1000+Theorems/Item-based query
- 1000+Theorems/RelationsWithinTheoremList
- 1000+Theorems/Seeding list
- 1000+Theorems/TheoremRelations
- 1000+Theorems/Wikidata lists
- 1000+Theorems/Wikidata lists/Theorems listed as part of (P527) of project Q128207330 and formalizations
- 1000+Theorems/Wikidata lists/Theorems present in Q944443 and formalizations
- Erdős number
- Integraality
- Participants
- Talks
- Talks/DMV2023
- Talks/DMV2023/Mathematics and Wikidata
- Wikidata lists
- Wikidata lists/Main subjects (P921) of works with a zbMATH document ID (P894)
- Wikidata lists/Methods used (P4510) by people with a zbMATH author ID (P1556)
- integers
Related WikiProjects
[edit]Wikidata
[edit]- Shared symmetry properties (crystallography):

















![{\displaystyle {\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/187f33664b79492eedf4406c66d67f9fe5f524ea)









